Parametric mean estimation

A common task in data science is mean estimation. The go-to estimator is sample mean, which is non-parametric in nature. But what if we have good reasons to believe in a parametric model for the population?

A common task: Mean estimation

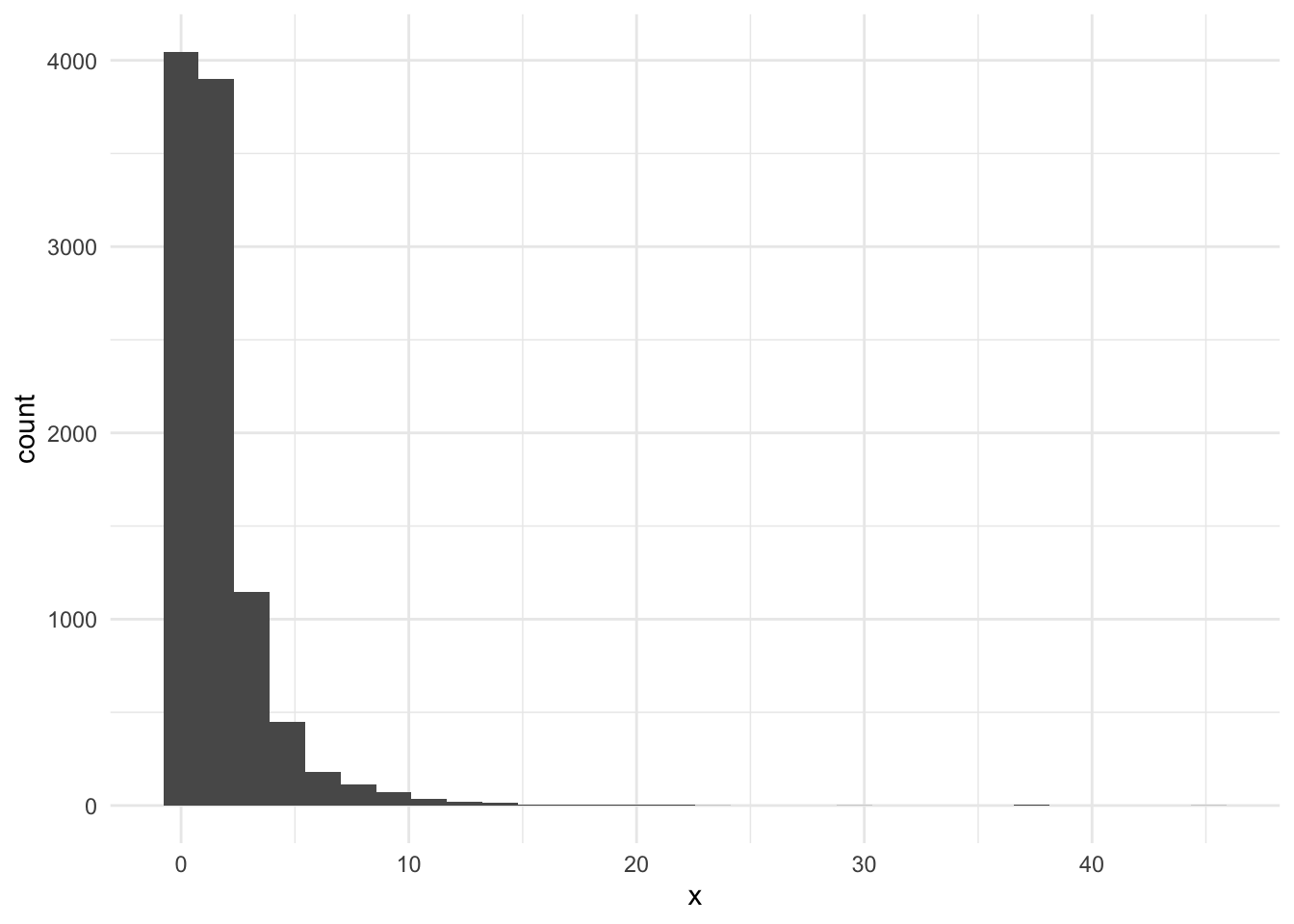
Suppose you are given i.i.d. samples \(X\) drawn from some unknown distribution and we wish to estimate its mean, \(\mathbb{E}[X]\). However being a good data scientist, you inspect the distribution \(X\) first, and saw the following histogram.

library(ggplot2)
theme_set(theme_minimal())

set.seed(1)
x <- exp(rnorm(1e4))
ggplot() + geom_histogram(aes(x = x))

That was not a great histogram that tells us little, since everything is just on the left. We decided to apply log transform and try again.

ggplot() + geom_histogram(aes(x = log(x)))

Now things are looking normal. But wait, we are supposed to find \(\mathbb{E}[X]\), not \(\mathbb{E}[\log(X)]\). Sample mean looks like it has a lot of variance. On the other hand, the log-transformed samples are looking really normally distributed. If we are willing to believe that \(\log(X) \sim N(\mu, \sigma^2)\), can we do better?

Setup

Suppose we want to model \(X\) as \(X = h(Z)\) for some \(Z \sim N(\mu, \sigma^2)\). This is perhaps believable after staring at histograms for hours, or perhaps \(X\) themselves are suppose to be normally distributed by Central Limit Theorem, but it’s not quite there yet. In the example above, \(h(Z) = \exp(Z)\).

Now we have two estimators of \(\mathbb{E}[X]\). One is sample mean (the non-parametric one), \[\frac{1}{n} \sum_{i = 1}^n X_i,\] and the other one is the parametric one \[f(\hat{\mu}, \hat{\sigma}) \coloneqq \mathbb{E}_{Z \sim N(\hat{\mu}, \hat{\sigma}^2)}[h(Z)],\] where \((\hat{\mu}, \hat{\sigma})\) can be estimated via your favorite method which is probably maximum-likelhood in this case.

Unless \(h\) is something weird, both are probably consistent. The parametric estimator may be biased, but that is a risk I am willing to take. How are their efficiencies?

Intuitively, the parametric one should be more efficient. We are supplying extra structure to the problem (the parametrization) and giving up unbiasedness. We must be gaining something, right?

Efficiency

Let’s analyze the simpler one, the non-parametric estimator. The asymptotic variance, scaled appropriately by \(n\), is \(\text{var}(h(Z)) = \mathbb{E}[h(Z)^2] - [\mathbb{E} h(Z)]^2\).

For the parametric one, the asymptotic variance of maximum likelihood estimator \((\hat{\mu}, \hat{\sigma})\) is the inverse of the Fisher information matrix \[\begin{pmatrix} \sigma^2 & 0 \\ 0 & \sigma^2 / 2\end{pmatrix}.\] The estimator \((\hat{\mu}, \hat{\sigma})\) is also asymtotically normal, so we can apply delta method to get the asymptotic variance of \(f(\hat{\mu}, \hat{\sigma})\). The remaining work is to find the gradient of \(f\).

We write the partial derivative out, swap it with the integral, then apply Stein’s lemma to get \[ \begin{align*} \frac{\partial}{\partial \mu} \mathbb{E}[h(Z)] &= \frac{\partial}{\partial \mu} \int h(z) \frac{1}{\sigma \sqrt{2\pi}} \exp\left(-\frac{(z - \mu)^2}{2 \sigma^2}\right) \,dz \\ &= \int h(z) \frac{1}{\sigma \sqrt{2\pi}} \frac{z - \mu}{\sigma^2} \exp(\cdots) \,dz \\ &= \frac{1}{\sigma^2} \mathbb{E}[h(Z)(Z - \mu)] \\ &= \mathbb{E}[h'(Z)]. \end{align*} \] In retrospect, I probably could have skipped the integral, since moving \(\mu\) is the same as moving \(X\).

Let’s try to be smarter with the other partial derivative. \[ \begin{align*} \frac{\partial}{\partial \sigma} \mathbb{E}[h(Z)] &= \lim_{\tau \to \sigma} \frac{1}{\tau - \sigma} \left[\mathbb{E}_\tau[h(Z)] - \mathbb{E}_\sigma[h(Z)]\right] \\ &= \lim_{\tau \to \sigma} \frac{1}{\tau - \sigma} \left[\mathbb{E}_\sigma\left[h\left(\frac{\tau}{\sigma} Z + \frac{\sigma - \tau}{\sigma} \mu\right)\right] - \mathbb{E}_\sigma [h(Z)]\right] \\ & = \lim_{\tau \to \sigma} \frac{1}{\tau - \sigma} \left[\mathbb{E}\left[h'(Z) \frac{\tau - \sigma}{\tau} (Z - \mu)\right]\right] \\ & = \frac{1}{\sigma} \mathbb{E}[h'(Z) (Z - \mu)] \\ & = \sigma \mathbb{E}[h''(Z)]. \end{align*} \]

So the asymptotic variance, scaled again by \(n\), is \[ \sigma^2 [\mathbb{E} h'(Z)]^2 + \frac{\sigma^4}{2} [\mathbb{E} h''(Z)]^2. \]

Here are some simple cases.

\(h(z)\)	Non-parametric	Parametric
\(z\)	\(\sigma^2\)	\(\sigma^2\)
\(z^2\)	\(4 \mu^2 \sigma^2 + 2 \sigma^4\)	\(4 \mu^2 \sigma^2 + 2 \sigma^4\)
\(z^3\)	\(9 \mu^4 \sigma^2 + 36 \mu^2 \sigma^4 + 15 \sigma^6\)	\(9 \mu^4 \sigma^2 + 36 \mu^2 \sigma^4 + 9 \sigma^6\)
\(z^4\)	\(16 \mu^6 \sigma^2 + 168 \mu^4 \sigma^4 + 384 \mu^2 \sigma^6 + 96 \sigma^8\)	\(16 \mu^4 \sigma^2 + 132 \mu^4 \sigma^4 + 216 \mu^2 \sigma^4 + 36 \sigma^8\)
\(\exp(z)\)	\((e^{\sigma^2} - 1)\exp(2\mu + \sigma^2)\)	\((\sigma^2 + \sigma^4 / 2) \exp(2\mu + \sigma^2)\)

While the parametric variance is smaller, it is hard to say how much we gain from trading away the unbiasedness. If \(\sigma / \mu \ll 1\), then these two are really the same. But in that case, delta method gives a good approximation and \(X\) would pretty much look normal.

Questions

1. Is the non-parametric variance always at least that of the parametric one? It looks like that is the case above, but I do not know for sure.
2. It makes sense that the two variances are the same for \(h(z) = z\), but why is that the case for \(h(z) = z^2\) as well? Is there something special about taking squares?